Dung[eon] at a Turn in the Road

I’ve become aware of some issues, as should be expected in a new venture. The question is what to do about them.

I started this series because a small Zoom Ensemble I’ve been hanging with is working on a dungeon program that’s being created by one of the ensemble members, and it seemed like an interesting problem for me and Codea. So I decided to work a bit on my own version of the basic dungeon game idea.

Now other than a few games, Colossal Cave, which was a pure text game, and some similar ones, like Zork, and of course Doom, I’ve not really played much in the roguelike game world, much less thought about how to implement such a game. I like to think that brings me in with no preconceptions, but what it really brings in is huge tracts, not of land, but of ignorance.

Now I do these little programs and articles because they interest me. As the many thousands of people who do not read these articles know, my Codea activities aren’t necessarily interesting to anyone else. That’s kind of OK with me. I’m just a lonely boy coding and scribing into the darkness.

The biggest problems in software development, be it “agile” or other, are surely large systems that have been around and worked on for a long time. “Brownfield” as opposed to greenfield, as some would have it. I’m not interested in that. I enjoy working the code under my graceful and delicate touch, bringing things into existence that haven’t existed before, and shaping them, often again and again, until I get them as close to just right as I can.

Or, just slightly less poetically, the part of this work that appeals to me is the work that takes place in small calm pockets where we can see what’s going on and move things around as needed.

I do believe that what happens here is not unlike what happens in a big brown pile of legacy um code, at least if we work to have that code reasonably well crafted. The reason is that even a very large program is best created as an assembly of small pieces, each one doing its job, with the pieces connected together in a loose and flexible fashion.

When code is like that, everything looks like things look here: small, and manageable. When things don’t look like that, the first order of business should be to make them look more like that. Be that as it may, I like to solve things in a space like this one, where they are small enough for us all to understand, yet large enough to be interesting.

I like to solve them from scratch. That’s not to say that I don’t research approaches and resources. You’ll have seen that I’ve even studied the assembly code for the games like Asteroids and Space Invaders that I’ve replicated here. But I don’t drag in the code and convert it to Codea. I write new code that does the thing in ways that make sense with my current thinking and tool set.

Which brings us to

Dung[eon]

I’ve read enough about dungeon creation to be aware that there’s some real math and technology in use in some of the best games. Delaunay triangulation, which generates paths between points, touching all points and never crossing a line. Minimal spanning trees, which reduce paths to the minimum number needed to get everywhere. Maze generators. And so on.

There’s source code for all these bits of dungeon tech, and even for entire games. I could convert a game, or an algorithm, and be good to go. And I don’t want to do that if I can avoid it.

I’d really rather work as if those resources weren’t there to be copied, though there might be write-ups and articles and such. I’d rather work without the high-tech math tools. I’d like to discover what creating a game is like, not read about it and regurgitate it. And when I work that way, learning happens, often when I least expect it.

That has happened with the D1 version of my Dung[eon] program.

I’ve had some interesting success with the idea of placing room rectangles in a small space, overlapping as they will, and then moving them apart, essentially by making them detest each other. I used the separation logic from flock simulation to do that, and it works nicely.

But there’s a problem–or I think there is. Maybe I’m wrong. But there’s at least an issue.

Many roguelike games are created on a grid of tiles, floor tiles, wall tiles, and so on. Here’s a picture of the screen of “Simple Dungeon”, a Codea program by “Mark” of the Codea forum. You can see the squares that make up the space. Everything is based on those squares and aligned to them.

My dungeon rooms start out on integer coordinates and are of integer sizes, so they could easily be tiled. Scale everything up by some amount X and tile with tiles of side X. Should work fine. But there’s trouble brewing.

The separation logic can be thought of as applying a force to a room, based on the sum of forces from its neighbors. These forces net out, and the room nudges over a bit. As you’ve seen in the videos, this works nicely and in a kind of amusing way.

But the rooms don’t end up on integer coordinates when we’re done. So if two rooms were side by side, their tiling might not match up. If there was a hallway between them, its tiles might not match either of the rooms.

I tried forcing the separation logic to move the rooms only to integer positions, and the effect of that was interesting: quite often, the rooms don’t completely separate. Sometimes a bunch of rooms stays stuck together. The reason, I believe, is that because of the rounding, opposing forces can more easily balance, so a room stays trapped where it is.

My current scheme relies on being able to separate the rooms and it’s not even the hard part of what’s before us: carving the paths between them is going to be harder. So I am wondering what to do. There are many possibilities, I suppose, but they include at least:

1. Let the rooms fall where they may and don’t use tiled flooring;
2. Adjust the rooms to integer coordinates at the last minute;
3. Start over.

I hadn’t thought of idea number two until I started writing this stuff. It’s actually helpful to try to put things down on “paper”, though I can tell you it is time-consuming. But the thinking part, that’s worth while. And telling the story helps.

So I think I’ll change plans. I was going to have justified starting over by now in the article, and then to start over. Instead, let’s put the rooms back on integer coordinates when the separation is complete.

I think I’ll set that up to be done on a touch, so that we can watch it happen.

function touched(touch)
    if touch.state == ENDED then
        Room:setToInteger(Rooms)
    end
end

That’s easy enough, except for the setToInteger part. I’ll have to write that:

function Room:setAllToInteger(rooms)
    for i,r in ipairs(rooms) do
        r:setToInteger()
    end
end

In writing it, I realized that I wanted setToInteger to be the room method, so I renamed the class method to setAllToInteger. And, mysteriously, I remembered to change the touched. Now then:

function Room:setToInteger()
    self.x = math.ceil(self.x)
    self.y = math.ceil(self.y)
end

That will move everyone in the same direction, northeast, since all our coordinates are positive. Now to see what happens. With luck, we won’t notice at all.

Yes. It works so nicely, in fact, that showing you a video of if would be a waste of bits. You can barely see anyone move at all. Which you’d expect, since they’re moving about half a pixel on the average. You can just see a sort of jiggle, or if you focus on a particular gap you might see it get a tiny bit larger or smaller.

Now I’d like to build that in to the current process, as strange as that process is. So we’ll do that when the moving has converged. Right now that’s in Main’s draw, changed to be like this:

function draw()
    if CodeaUnit then showCodeaUnitTests() end
    pushMatrix()
    pushStyle()
    rectMode(CENTER)
    for i,r in ipairs(Rooms) do
        r:draw()
    end
    if AdjustCount > 0 then
        if ElapsedTime - AdjustTime > AdjustDelay then
            AdjustTime = ElapsedTime
            AdjustCount = Room:adjustAll(Rooms)
            if AdjustCount == 0 then
                Room:setAllToInteger(Rooms)
            end
        end
    end
    popStyle()
    popMatrix()
end

Well, that was a long way to go for three lines of code, one of which was end, but it’s a load off my mind. Here’s a typical picture of a 50 room dungeon at present:

Now the main problem on my mind has been connecting these rooms together so that you can march through the entire dungeon, slaying monsters and collecting treasure, or whatever dungeon adventurers do, none of my business really. So let’s focus back on that.

I was working on adjacency, you’ll remember, and I threw away my first cut at it, and was working on a second approach, hopefully one that would actually work. We finished up yesterday with a stack object that I expect to need, and with two functions xOverlap and yOverlap that tell us how far two rooms overlap along x-oriented or y-oriented walls.

My plan for those is to find neighboring rooms with sufficient overlap to allow for a door. Then, recursively or semi-recursively, we can find all the rooms that are connectable to a given room. I though I’d color those some color, to get a sense of how connectable the maze would be. If it’s good enough, we could just throw away any unconnected rooms and carry on.

Adjacency Yet Again

So my rough idea is that two rooms are adjacent if

*Their north-south or south-north sides are close enough together and there is sufficient x-axis overlap, or

• Their east-west or west-east sides are close enough together and there is sufficient y-axis overlap.

My experience in doing this has mostly consisted of doing it wrong, so I think we’ll TDD this. First the sides close enough part:

        _:test("east west close enough", function()
            local e = Room:fromCorners(100,100,200,200)
            local w = Room:fromCorners(201,100,301,200)
            expect(e:closeEnough(w)).is(true)
        end)

I’m really glad I did that fromCorners room creation method, it makes this job at least possible. I’m pretty sure that oh hell. Room w is east of room e. Rename. (Darn, I suck sometimes.)

        _:test("east west close enough", function()
            local w = Room:fromCorners(100,100,200,200)
            local e = Room:fromCorners(201,100,301,200)
            expect(e:closeEnough(w)).is(true)
        end)

I’m not sure what I’ll use for the value of close enough but 1 has to work. They can’t be closer than that.

We are not surprised to see this test fail with a missing function closeEnough. Therefore:

Wait. This is the east-west version of close enough. The method should be ewCloseEnough. Renaming.

OK, I think this:

function Room:ewCloseEnough(aRoom)
    hisWest = aRoom:west()
    myEast = self:east()
    return hisWest > myEast and hisWest-myEast < Room:closeEnough()
end

function Room:closeEnough()
    return 3
end

This is going to fail for the wrong reason. I think the call is reversed. Run it. Oh, and I forgot to write east and west.

function Room:east()
    return self.cx + self:halfWidth()
end

function Room:west()
    return self.cx - self:halfWidth()
end

I still expect a fail. Again a surprise. The center points aren’t named cx, they are named x.

Then I missed the _: in the test. Fixed:

        _:test("east west close enough", function()
            local w = Room:fromCorners(100,100,200,200)
            local e = Room:fromCorners(201,100,301,200)
            _:expect(e:ewCloseEnough(w)).is(true)
        end)

Finally the error I expect:

12: east west close enough  -- Actual: false, Expected: true

Now I think if I reverse the call, the test should run:

        _:test("east west close enough", function()
            local w = Room:fromCorners(100,100,200,200)
            local e = Room:fromCorners(201,100,301,200)
            _:expect(w:ewCloseEnough(e)).is(true)
        end)

And it does. But it should work both ways, so we’ll test both ways to drive out the other branch:

        _:test("east west close enough", function()
            local w = Room:fromCorners(100,100,200,200)
            local e = Room:fromCorners(201,100,301,200)
            _:expect(w:ewCloseEnough(e)).is(true)
            _:expect(e:ewCloseEnough(w)).is(true)
        end)

And that fails again of course and we fix:

function Room:ewCloseEnough(aRoom)
    local ce = Room:closeEnough()
    local hisE = aRoom:east()
    local hisW = aRoom:west()
    local myE = self:east()
    local myW = self:west()
    return (hisW>myE and hisW-myE<ce) or (myW>hisE and myW-hisE<ce) 
end

I renamed all the locals to shorter names to make that final expression more readable. That may or may not have worked. But the function works and that’s good. Let’s do N-S and then see what we have.

        _:test("north south close enough", function()
            local s = Room:fromCorners(100,100,200,200)
            local n = Room:fromCorners(100,201,100,301)
            _:expect(n:nsCloseEnough(s)).is(true)
            _:expect(s:nsCloseEnough(n)).is(true)
        end)

And …

function Room:nsCloseEnough(aRoom)
    local ce = Room:closeEnough()
    local hisN = aRoom:north()
    local hisS = aRoom:south()
    local myN = self:north()
    local myS = self:south()
    return (hisS>myN and hisS-myN<ce) or (myS>hisN and myS-hisN<ce)
end

With suitable definitions of north and south:

function Room:north()
    return self.y + self:halfHeight()
end

function Room:south()
    return self.y - self:halfHeight()
end

Test runs. Is it good enough? I think so, it’s just checking whether the coordinates are close enough together. I wonder if we could improve the code or remove the massive duplication.

Could I judiciously use absolute value of the coordinate differences to avoid the check for e.g. hisS>myN, which is basically asking if he’s above me. If he were below then the difference hisS-myN would be negative … and far less than ce. No, I think I’ll leave this alone for now and try to apply it.

Now I want a function, maybe r1:isNeighbor(r2), true if they’re close enough by this definition, and their overlap is how much? Our rooms are around 50 or more in width and height. Let’s say overlap has to be at least 10.

Can I be forgiven for just coding up isNeighbor without TDDing it? I’m really tired of ginning up examples. Let’s do it and see how much trouble we get in. Should be plenty.

Neighbors

Two rooms are neighbors if:

function Room:isNeighbor(aRoom)
    local doorWidth = 10
    return (self:nsCloseEnough(aRoom) and self:xOverlap(aRoom)>doorWidth()) or
           (self:ewCloseEnough(aRoom) and self:yOverlap(aRoom)>doorWidth)
end

Yes, I just pulled that out of my um hat. Now, for a first step, let’s color all the rooms adjacent to room 1 red. We’ll do that like this:

function draw()
    if CodeaUnit then showCodeaUnitTests() end
    pushMatrix()
    pushStyle()
    rectMode(CENTER)
    for i,r in ipairs(Rooms) do
        r:draw()
    end
    if AdjustCount > 0 then
        if ElapsedTime - AdjustTime > AdjustDelay then
            AdjustTime = ElapsedTime
            AdjustCount = Room:adjustAll(Rooms)
            if AdjustCount == 0 then
                Room:setAllToInteger(Rooms)
                Room:colorNeighborsOf(1, Rooms, color(255,0,0,100))
            end
        end
    end
    popStyle()
    popMatrix()
end

And:

function Room:colorNeighborsOf(aRoomNumber, rooms, aColor)
    local me = rooms[1]
    me:setColor(aColor)
    for i,r in rooms do
        if r:isNeighbor(me) then
            r:setColor(aColor)
        end
    end
end

I don’t think I’m going to like this calling sequence but it’ll do for now, Now we need to have a color and set it.

function Room:init(x,y,w,h)
    self.number = 666
    self.color = color(0,255,0,25)
    self.x = x or math.random(WIDTH//4,3*WIDTH//4)
    self.y = y or math.random(HEIGHT//4,3*HEIGHT//4)
    self.w = w or math.random(WIDTH//20,WIDTH//10)
    self.h = h or math.random(HEIGHT//20,WIDTH//10)
end

function Room:setColor(aColor)
    self.color = aColor
end

function Room:draw()
    pushMatrix()
    fill(255)
    stroke(255)
    strokeWidth(0)
    textMode(CENTER)
    translate(self.x,self.y)
    local nr = string.format("%d", self.number)
    text(nr,0,0)
    fill(self.color)
    stroke(0,255,0)
    strokeWidth(2)
    rect(0,0, self.w, self.h)
    popMatrix()
end

Room:215: attempt to call a table value
stack traceback:
	Room:215: in method 'colorNeighborsOf'
	Main:36: in function 'draw'

Forgot ipairs as I so often do:

function Room:colorNeighborsOf(aRoomNumber, rooms, aColor)
    local me = rooms[1]
    me:setColor(aColor)
    for i,r in ipairs(rooms) do
        if r:isNeighbor(me) then
            r:setColor(aColor)
        end
    end
end

Well. I really think room 47 should be red too. I wonder why it’s not.

Now this is a signal that I have something wrong and probably shouldn’t try to debug it so much as back up and write some tests. But first I want some information, so I’m going to implement a little debug print that I can call:

function Room:dump()
    print(self:south(), self:north(), self:east(), self:west())
end

Now I’ll run again, which will give us a new picture, but we can ask a question or two. But wait, an error:

Room:183: attempt to call a number value (local 'doorWidth')
stack traceback:
	Room:183: in method 'isNeighbor'
	Room:216: in method 'colorNeighborsOf'
	Main:36: in function 'draw'

Maybe that happened before and I didn’t see it.

function Room:isNeighbor(aRoom)
    local doorWidth = 10
    return (self:nsCloseEnough(aRoom) and self:xOverlap(aRoom)>doorWidth) or
           (self:ewCloseEnough(aRoom) and self:yOverlap(aRoom)>doorWidth)
end

Now we’re getting more than one, but we still missed room 7 here. Here’s room 1, then 7:

640.5	739.5	371.0	251.0
509.5	640.5	403.5	312.5

OK, we see some issues with the dump, should include the room number if we have it, and should be in corners order. I think I’ll fix it and then get another example.

function Room:dump()
    print(self.number, self:south(),self:west(), self:north(), self:east())
end

OK, here we missed room 16. Values are:

1	470.5	1054.0	579.5	1190.0
16	579.5	1059.5	672.5	1150.5

We see room 16 as north of 1 with lots of overlap. In fact, however, they have the same edge coordinate, 579.5. This can happen because of odd room sizes and the concomitant rounding. Our closeEnough function doesn’t allow for the values to be equal. We fix that:

function Room:ewCloseEnough(aRoom)
    local ce = Room:closeEnough()
    local hisE = aRoom:east()
    local hisW = aRoom:west()
    local myE = self:east()
    local myW = self:west()
    return (hisW>=myE and hisW-myE<ce) or (myW>=hisE and myW-hisE<ce) 
end

function Room:nsCloseEnough(aRoom)
    local ce = Room:closeEnough()
    local hisN = aRoom:north()
    local hisS = aRoom:south()
    local myN = self:north()
    local myS = self:south()
    return (hisS>=myN and hisS-myN<ce) or (myS>=hisN and myS-hisN<ce)
end

Then run again:

Here’s one that looked like it should work. Maybe the overlap wasn’t enough:

1	517.5	359.5	632.5	450.5
15	612.5	450.0	713.5	540.0

The room is to the east of #1, oh and look, his starting x, 450, is less than #1’s ending x, 450.5. He should have been seen as intersecting. If he is, our neighbors thing can’t work: it assumes no overlap. This should make a good test for intersection.

        _:test("intersect bug", function()
            local r1 = Room:fromCorners(517.5,359.5,632.5,450.5)
            local r2 = Room:fromCorners(612.5,450.0,	713.5,540.0)
            _:expect(r1:intersects(r2)).is(true)
        end)

I’d like this to fail. Does it?

No, it succeeds. Then why did we stop moving rooms? We don’t stop until no one moves. Oh, and then we round. We moved him back into intersecting, I’ll bet. Let’s remove the rounding thing and decide that it doesn’t matter, then see what our adjacent rooms seem to be.

This seems to be working now. Let’s now find all the rooms we can reach from #1. Now I built that cool stack object but should we try for a recursive solution just because it would be cool? No, we shouldn’t. So let’s do.

We start with a room. For each of its neighbors, if it is not colored red, we color it red, then tell it to color its neighbors. When we are out of neighbors, we return.

This algorithm may not be terribly fast, since it will check all the rooms in the space all the time. Some kind of quad tree sort of thing would be good, but no. We’ll just let ‘er rip.

First few tries will probably blow the stack. We’ll be careful. Won’t we? Won’t we?

I replaced the other coloring method with this one that is room-based:

function Room:colorNeighborsIn(rooms, aColor)
    self:setColor(aColor)
    for i,r in ipairs(rooms) do
        if r:isNeighbor(self) and r:getColor() ~= aColor then
            r:colorNeighborsIn(rooms, aColor)
        end
    end
end

Sent to a room, it colors the room, then searches all the rooms in the room collection for neighbors, and as it finds them, it tells them to color themselves and their neighbors. What could go wrong?

Change the code in draw (where this definitely does not belong).

function draw()
    if CodeaUnit then showCodeaUnitTests() end
    pushMatrix()
    pushStyle()
    rectMode(CENTER)
    for i,r in ipairs(Rooms) do
        r:draw()
    end
    if AdjustCount > 0 then
        if ElapsedTime - AdjustTime > AdjustDelay then
            AdjustTime = ElapsedTime
            AdjustCount = Room:adjustAll(Rooms)
            if AdjustCount == 0 then
                --Room:setAllToInteger(Rooms)
                Rooms[1]:colorNeighborsIn(Rooms, color(255,0,0,100))
            end
        end
    end
    popStyle()
    popMatrix()
end

I’m gonna run it. Stand well back.

First result makes me laugh:

Well, it worked. Stand back again.

Now that’s what I’m talkin about! Look at that coverage! We’ve covered 42 out of 50 rooms. It looks good to me, though I kind of wonder how Room 5 got marked. Probably it’s close enough to room 15. This makes me want to draw the path between the rooms. Let me commit this, it’s pretty good. Commit: recursive coloration.

For the lines, let’s just make a table of … well, let’s do a line class. We’ll just code it up, we’re hot. None of that wussy TDD stuff for us no sir.

function Room:colorNeighborsIn(rooms, aColor)
    self:setColor(aColor)
    for i,r in ipairs(rooms) do
        if r:isNeighbor(self) and r:getColor() ~= aColor then
            table.insert(Lines, self.x,self.y, r.x,r.y)
            r:colorNeighborsIn(rooms, aColor)
        end
    end
end

Now this, ladies and gentlemen, cats and dogs (living together), this is what I’m talkin about:

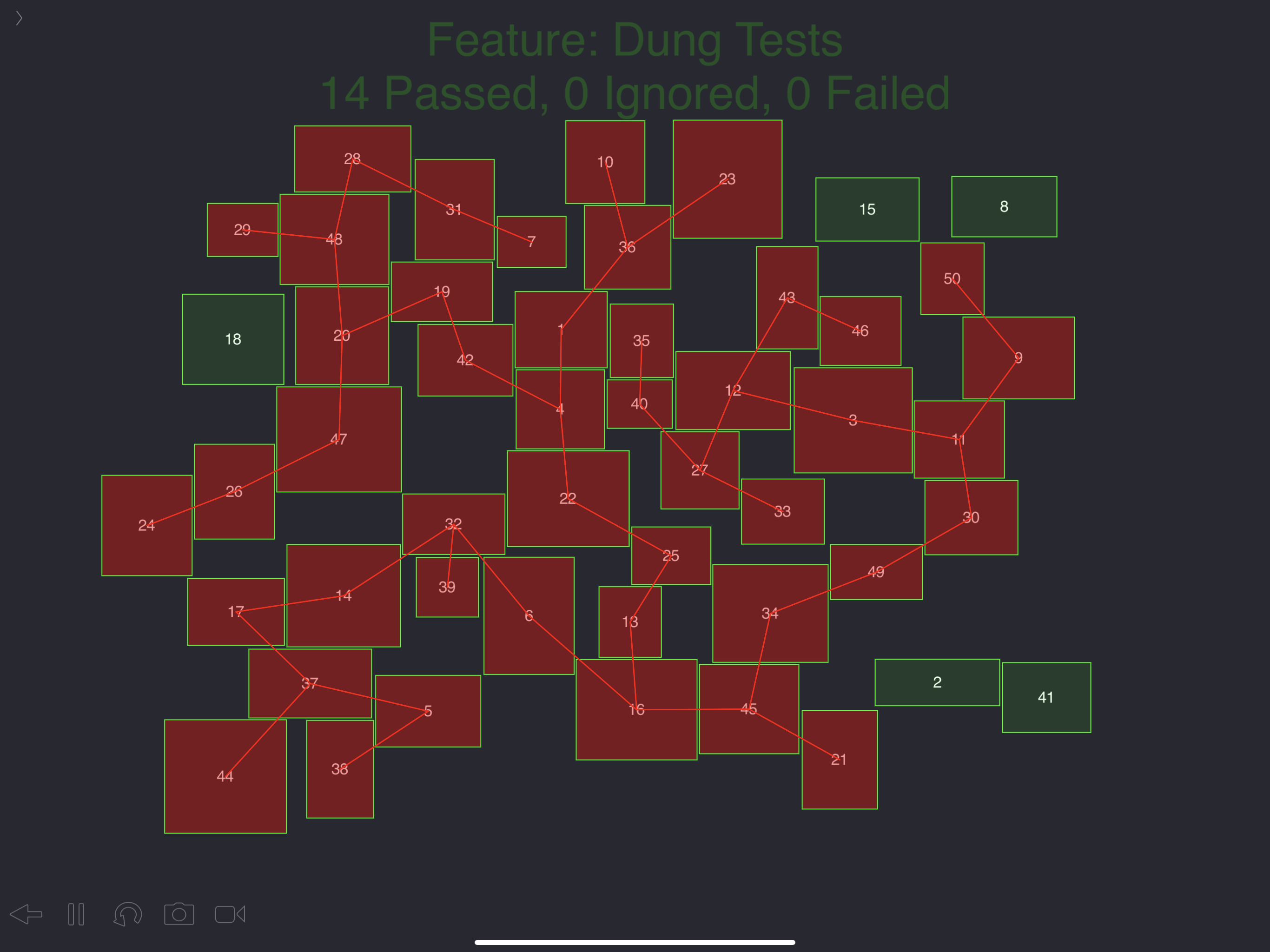
What we have here is all the rooms connecting to room 1, recursively, by one path. There are no loops in this graph, but there are unquestionably loops available if we put doors in some of the rooms that are adjacent in other ways. In the last picture above, note for example rooms 3 and 46, around 2 o’clock. They are clearly adjacent but our tree search found them on separate branches. Probably we went from 11 to 3 to 12 to 43 to 46. When we recurred down 46, 3 was taken so we didn’t count that a legit path. We could keep track of candidates not taken, and put a few of them in to make loops. We’ll worry about that later–much later. I do want to change the lines table. I want each Line to contain two Rooms, not the coordinates. I think that will be handy later. Let’s rename the class to Neighbor, and the collection to Neighbors:

-- Neighbor
-- RJ 20201106

Neighbor = class()

function Neighbor:init(room1, room2)
    self.room1 = room1
    self.room2 = room2
end

function Neighbor:draw()
    pushStyle()
    pushMatrix()
    stroke(255,0,0)
    resetMatrix()
    line(self.room1.x, self.room1.y, self.room2.x, self.room2.y)
    popStyle()
    popMatrix()
end

function Room:colorNeighborsIn(rooms, aColor)
    self:setColor(aColor)
    for i,r in ipairs(rooms) do
        if r:isNeighbor(self) and r:getColor() ~= aColor then
            table.insert(Neighbors, Neighbor(self, r))
            r:colorNeighborsIn(rooms, aColor)
        end
    end
end

function draw()
    if CodeaUnit then showCodeaUnitTests() end
    pushMatrix()
    pushStyle()
    rectMode(CENTER)
    for i,r in ipairs(Rooms) do
        r:draw()
    end
    if AdjustCount > 0 then
        if ElapsedTime - AdjustTime > AdjustDelay then
            AdjustTime = ElapsedTime
            AdjustCount = Room:adjustAll(Rooms)
            if AdjustCount == 0 then
                Rooms[1]:colorNeighborsIn(Rooms, color(255,0,0,100))
            end
        end
    end
    for i,l in ipairs(Neighbors) do
        l:draw()
    end
    popStyle()
    popMatrix()
end

So that worked out nicely. A good spot to stop, as it is 1018 and I’ve been at this since before 0700, with a break for a chai run.

Commit: path between Neighbors.

Let’s sum up.

Summing Up

So the big picture is that when I got here I was convinced that it was time to start over. Thinking about the options (and writing about them) caused me to invent the idea of aligning the rooms to integer coordinates at the last minute. I knew that could fudge with the overlap but I felt it would do no harm. I was picturing everyone kind of moving up and to the right.

But the big decision there was the one not to start over. I convinced myself that what we have wasn’t horribly broken and unable to work. So I went on with adjacency, because I was interested in how well connected the maze was, because to the eye it looks rather well connected.

Some TDD on adjacency paid off with working code that’s pretty tricky:

function Room:xOverlap(aRoom)
    sLo,xx,sHi,xx = unpack(self:corners())
    rLo,xx,rHi,xx = unpack(aRoom:corners())
    return max(min(sHi,rHi)-max(sLo,rLo),0)
end

function Room:yOverlap(aRoom)
    xx,sLo,xx,sHi = unpack(self:corners())
    xx,rLo,xx,rHi = unpack(aRoom:corners())
    return max(min(sHi,rHi)-max(sLo,rLo),0)
end

function Room:ewCloseEnough(aRoom)
    local ce = Room:closeEnough()
    local hisE = aRoom:east()
    local hisW = aRoom:west()
    local myE = self:east()
    local myW = self:west()
    return (hisW>=myE and hisW-myE<ce) or (myW>=hisE and myW-hisE<ce) 
end

function Room:nsCloseEnough(aRoom)
    local ce = Room:closeEnough()
    local hisN = aRoom:north()
    local hisS = aRoom:south()
    local myN = self:north()
    local myS = self:south()
    return (hisS>=myN and hisS-myN<ce) or (myS>=hisN and myS-hisN<ce)
end

function Room:isNeighbor(aRoom)
    local doorWidth = 10
    return (self:nsCloseEnough(aRoom) and self:xOverlap(aRoom)>doorWidth) or
           (self:ewCloseEnough(aRoom) and self:yOverlap(aRoom)>doorWidth)
end

Tricky but I’m confident in it. This is the way with geometry things, the code always comes down to weird comparisons on coordinates. And I always get confused between left and right east and west. So sue me. Anyway with the tests, I was and am confident that the checks are working.

Then I pulled recursive adjacency checking out of um the air, and it worked as expected–only if I removed the rounding. I was OK with that and still am. We’re only at most a half pixel off from an integer coordinate. The visual effect was negligible.

And then, I don’t know why this came to mind, I added in the lines between rooms, which produce a tree of connections from room 1 to everywhere that can be reached. No loops, just a tree. And we have a table of neighbors, the ones our recursive search finds. It doesn’t include neighboring pairs who were already found connected by a different path. We could probably get a collection of all neighbors easily enough, during this search or another one, if we want it.

And we might want it. Suppose our Neighbors table included the ones that want lines between them, because they were found in the recursive search, and also ones that were found but the found room was already colored. Those rooms would be candidates for extra doors, causing a few loops in the maze, which is thought to make them more interesting.

I switched suddenly from TDD on a bunch of nitty-gritty stuff to doing the recursive search and then the lines-neighbors thing by basically just typing them in. And they worked promptly, little or no confusion or debugging.

And honestly … the Lines or Neighbors class is so easy that one could hardly TDD it. The recursive search … setting up a test for that … I really don’t see right now how I could have done that in a practical fashion.

Maybe I “should” have stayed in TDD mode. Maybe I switched at just the right time. Had I gotten in trouble, maybe I’d have switched back, and found a way to test my way forward.

This sort of thing comes up all the time. As you’ll have seen if you follow this whole Codea series, Asteroids, Space Invaders, and now this, I tend not to use TDD as much as I might, and I tend often to get into trouble. I try to lean toward doing more TDD, because it helps me produce my little products with more ease and less debugging.

But I don’t hold myself to “Always use TDD”, and I wouldn’t expect you to hold yourself, or a manager to hold her employees to that rule. I expect that you’ll practice and learn good judgment, recognizing that the judgment we have at any moment in time isn’t the best possible, so that we’re continually adjusting.

When it comes to something that’s a bit hard to get into, and that remains hard to do sometimes, I recommend trying to learn toward doing it, because our lazy side and our uncreative side are often saying “nah, too hard”, when it would have been a good idea.

That, more exercise, less bad food, and all the other good habits. Yeah, we’re fine. And we can always use a little improvement.

See you next time!

D1